從turtle海龜動畫 學習 Python - 高中彈性課程系列 5 用函數封裝重複性指令-呼叫函數令烏龜畫正 n 邊形

目錄

• 5.5 用函數封裝重複性指令-呼叫函數令烏龜畫正 n 邊形
  • 匿名函數
  • 5.5.1 注意函數的局部變數 local variable 與全域變數 global variable 之互動狀況
• 以上可以等進階時再細看
  • 5.6 旋轉正多邊形_左下頂點為中心: 封裝為函數, 輸入引數: n 邊, m 重, side 邊長, 就會畫正 n 邊形左下頂點為中心 m 重旋轉之圖形
  • 5.7 旋轉正多邊形_左下頂點為中心 之型態實驗
    • 5.7.1 旋轉正3邊形
    • 5.7.2 旋轉正4邊形
    • 5.7.3 旋轉正5邊形
    • 5.7.4 旋轉正6邊形
    • 5.7.5 旋轉正7邊形
    • 5.7.6 旋轉正8邊形
    • 5.7.7 旋轉正9邊形

5.5 用函數封裝重複性指令-呼叫函數令烏龜畫正 n 邊形

Ref: 官網的文件: python-3.3.2-docs-pdf-a4

正規的函數定義法: An alternative is to just use the def statement and define a function in the usual way:

以下這個函數, 輸入 x,y 值, 會回應 x+y 的值

可以打開 IDLE 左上方 File/New File, 產生一個空白的類似小作家編輯器, 輸入以下程式碼, 再按 F5 執行編譯,

def adder(x, y): return x + y

# Ref: 官網的文件: python-3.3.2-docs-pdf-a4

def adder(x, y):
    return x + y

再在 IDLE consola 畫面, 輸入 adder(2,3) 等指令,

>>> adder(2,3)
5

以下是一個會計算兩倍的函數, 隨意取一個名稱叫 foo(),

def foo(x):
    foo1=2*x
    return foo1

在再 IDLE consola 畫面輸入 foo(4) 等指令, 就會回 4 的倍數 8, 給你, 執行畫面

>>> 
===== RESTART: C:/Users/user/Desktop/test.py =====
>>> foo(4)
8
>>> foo(40)
80

EX: 解析以下官網的文件的第二個例子, 預測執行時會得出甚麼結果

def print_assign(name, value):
    return name + ’=’ + str(value)

以下將上一節畫正五邊形的codes, 封裝為函數, 取名為 Pentagon( ) 以下 codes 存成 草稿檔 (script file), 取名為 regularPentagon.py 輸入 codes 完之後, 按 F5執行編譯, 就會畫出正五邊形

import turtle
T = turtle.Turtle()

def Pentagon(side):
    for i in range(5):
        T.forward(side)
        T.left(72)

Pentagon(100)

或是 按 F5執行之後, 再在 IDLE 輸入 >>>Pentagon(100) 就會畫出正五邊形

進一步修改成畫出正 n 邊形之函數 先計算出正 n 邊形之內角, 再計算出其外角,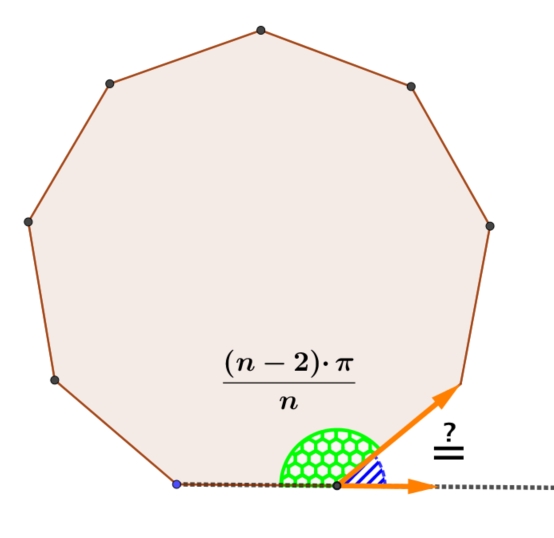

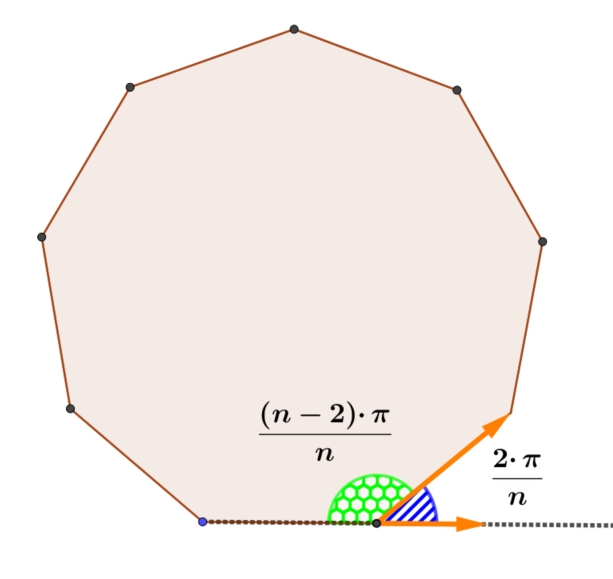
根據以上計算出之正 n 邊形之外角, $\frac{2\pi}{n}$ radian, 就可以直接修改上面畫正五邊形之函數, 改成為 畫正n邊形之函數, 如下

def regularPolygon(n, side):
    for i in range(n):
        T.forward(side)
        T.left(2*180/n)

接著, 我們可以進一步, 再用迴圈的概念, 呼叫上面定義好的畫正n邊形之函數, 形成雙重迴圈的概念, 定義一個函數 multiRegularPolygon(n, side), 對於輸入的 n, 畫出畫多重同邊正n邊形, 正3邊形到正 n 邊形.

def multiRegularPolygon(n, side):
    for i in range(3,n+1):
        regularPolygon(i, side)

接著, 我們也可以直接用雙重迴圈的概念, 不使用上面定義好的畫正n邊形之函數, 直接畫多重同邊正n邊形, 定義一個函數, 對於輸入的 n, 畫出正3邊形到正 n 邊形

def multiRegularPolygon_double_for(n, side):
    for i in range(3,n+1):
        for k in range(i):
            T.forward(side)
            T.left(2*180/i)

輸入 >>>multiRegularPolygon_double_for(30, 40) 就會畫出正3邊形到正 29 邊形

以下草稿檔有三個函數: 1 畫出正 n 邊形之函數, regularPolygon(n, side) 2 用雙重迴圈的概念, 定義一個函數, 對於輸入的 n, 畫出正3邊形到正 n 邊形, multiRegularPolygon_double_for(n, side) 3 用呼叫正 n 邊形之函數, 定義一個函數, 對於輸入的 n, 畫出正3邊形到正 n 邊形, multiRegularPolygon(n, side)

存成 script file, 取名為 multiRegularPolygon_double_for_loop.py 輸入完之後, 按 F5執行 會畫出正3邊形到正29邊形

import turtle
T = turtle.Turtle()
T.reset()
T.shape('turtle')
T.color('yellow','green')
turtle.bgcolor('black')
T.pensize(3)
T.penup()
T.goto(0,-100)
T.pendown()
#import math
def regularPolygon(n, side):
    for i in range(n):
        T.forward(side)
        T.left(2*180/n)

def multiRegularPolygon_double_for(n, side):
    for i in range(3,n+1):
        for k in range(i):
            T.forward(side)
            T.left(2*180/i)

    
def multiRegularPolygon(n, side):
    for i in range(3,n+1):
        regularPolygon(i, side)
        
multiRegularPolygon(29, 40)

• 以下可以等進階時再細看

  匿名函數

  lambda function 的定義法 adder = lambda x, y: x+y 超過1行就用 def 的方法

print_assign = lambda name, value: name + ’=’ + str(value)

Q: 函數可以輸入函數為引數嗎? (有時稱為”高階函數”, “泛函函數”) Ans: 可以 先定義一個函數: def test(f,n): return f(n)

再輸入 >>> test(lambda x: x**2,3) 9

5.5.1 注意函數的局部變數 local variable 與全域變數 global variable 之互動狀況

函數的局部變數 local variable 與全域變數 global varibale, 與一般語言 C, Java 等類似, 只要注意至少有一點與 C 不同:

注意 Python 與 C 不同之處, function 內無法更改 外部的全域變數, 例如迷宮之例子, 全域變數 maze, success, 參考本系列博文: 從 Logo 海龜繪圖 學習 Python - 高中彈性課程系列 11 用 turtle 呈現演算法之執行動作, https://blog.csdn.net/m0_47985483/article/details/111172062 link

必須在 function 內, 再加一個 global maze, 才能更改 maze.

如果沒宣告, 會無法更改 全域變數 maze, success 之值, 會出現以下之 error:

>>> 
,,,,,
UnboundLocalError: local variable 'success' referenced before ass

• 以上可以等進階時再細看

5.6 旋轉正多邊形_左下頂點為中心: 封裝為函數, 輸入引數: n 邊, m 重, side 邊長, 就會畫正 n 邊形左下頂點為中心 m 重旋轉之圖形

程式碼:

import turtle
T = turtle.Turtle()
T.clear()
T.home()
T.shape('turtle')
T.color('yellow','green')
turtle.bgcolor('black')
T.pensize(3)
T.penup()
#T.goto(0,-100)
T.pendown()
#import math
def regularPolygon(n, side):
    for i in range(n):
        T.forward(side)
        T.left(2*180/n)

    
def center_A_multiSameRegularPolygon(n, m, side):
    for i in range(1,m+1):
        regularPolygon(n, side)
        T.lt(360/m)

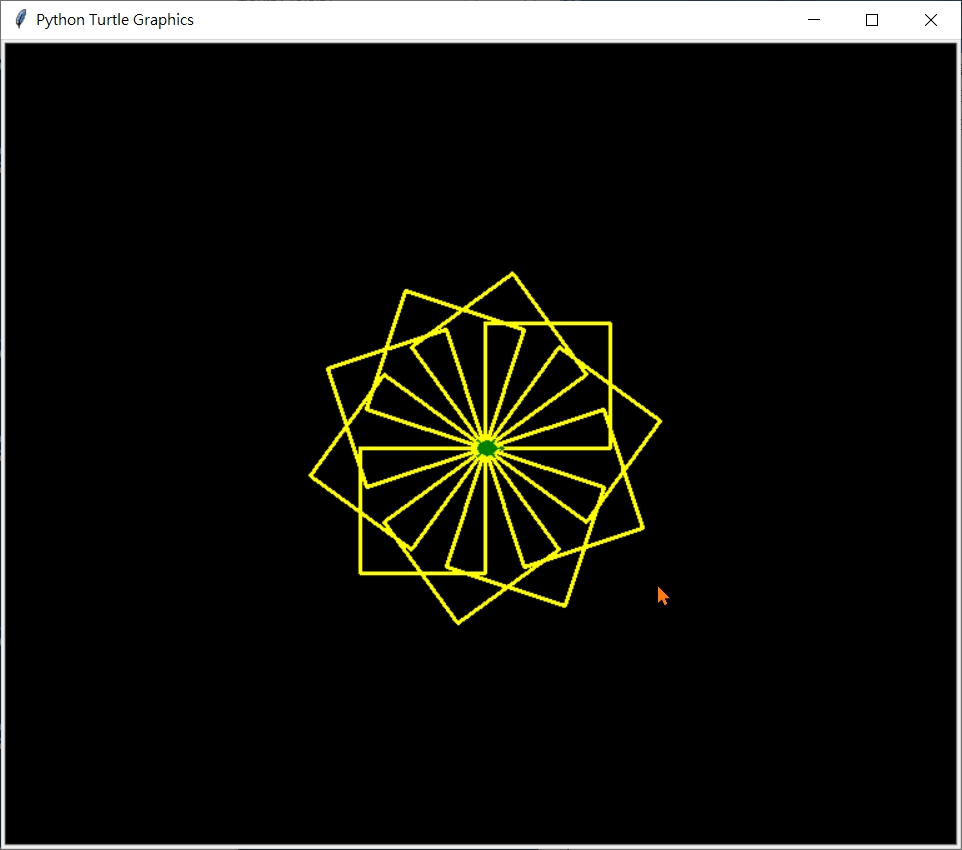
>>> center_A_multiSameRegularPolygon(6, 8, 50)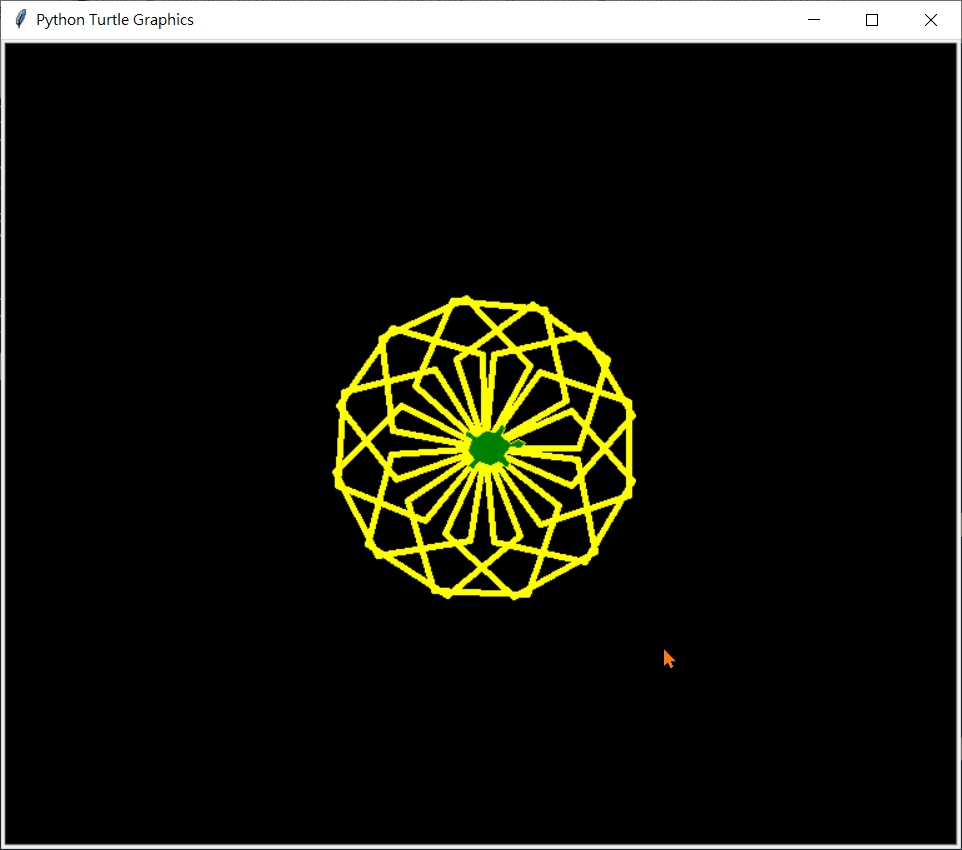

5.7 旋轉正多邊形_左下頂點為中心 之型態實驗

參考以下網站, , Dr. Kubeš - Galileo School 網址, 上課講義 DrawingGeometricShapes.pdf, 用 Scratch 畫旋轉正多邊形的各種圖案 Ref: https://sites.google.com/site/matejkubesgalileoschool/computer-science/ict-7ab-8a-scratch/learning-to-program-with-scratch/drawing-geometric-shapes link

5.7.1 旋轉正3邊形

以下旋轉正3邊形 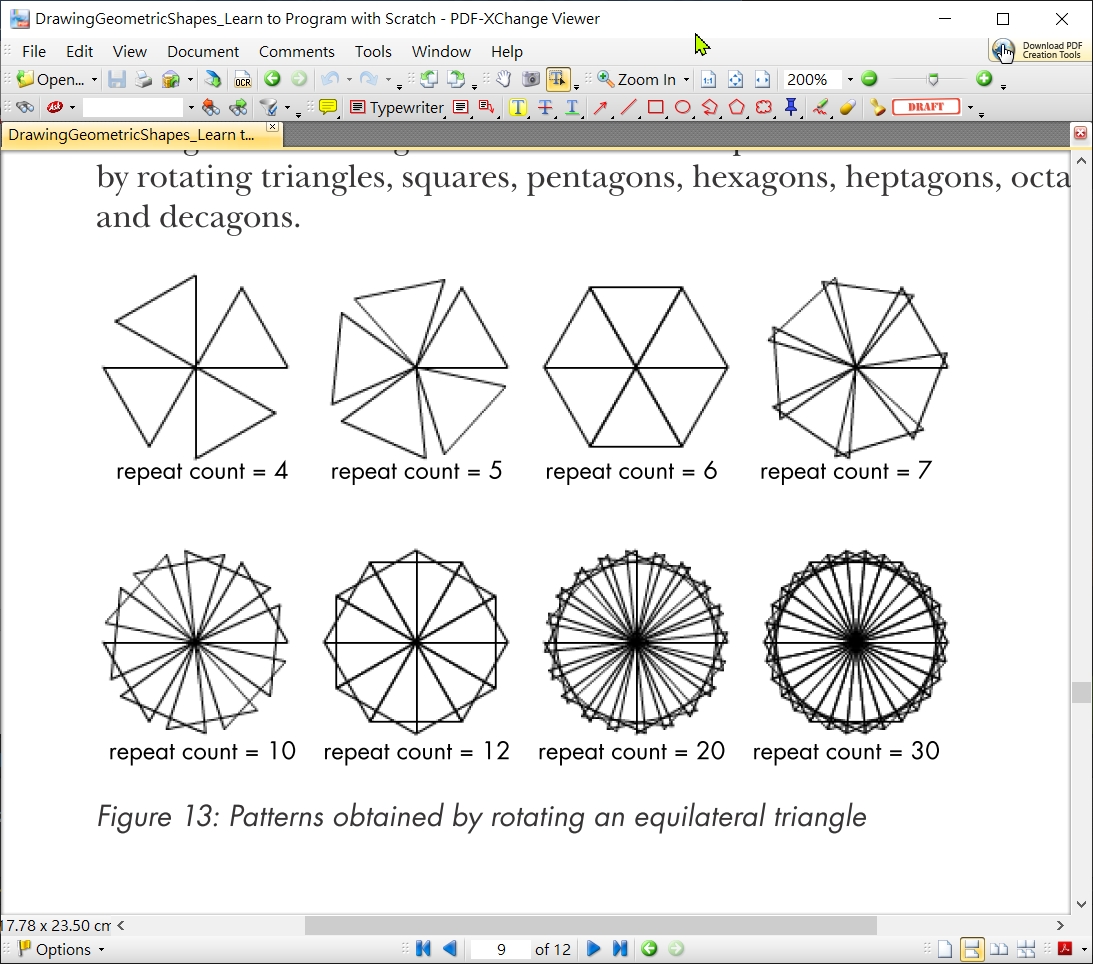旋轉正3邊形, 5重, 邊長100 >>>center_A_multiSameRegularPolygon(3, 5, 100)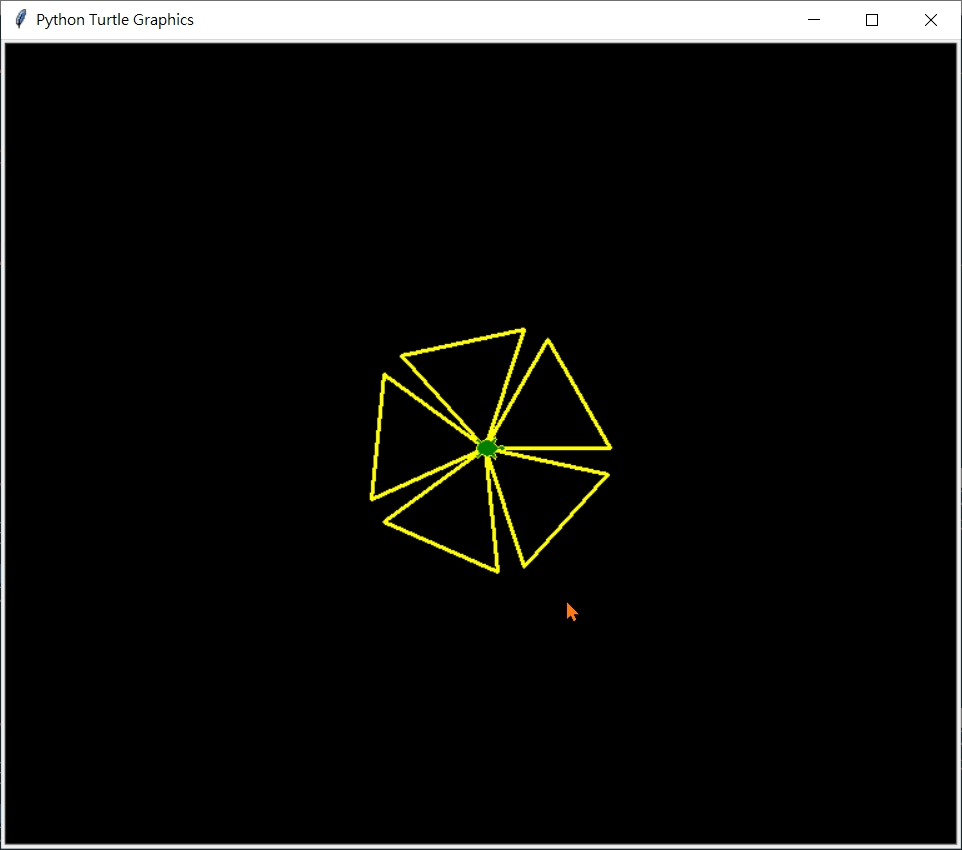

5.7.2 旋轉正4邊形

以下為旋轉正4邊形 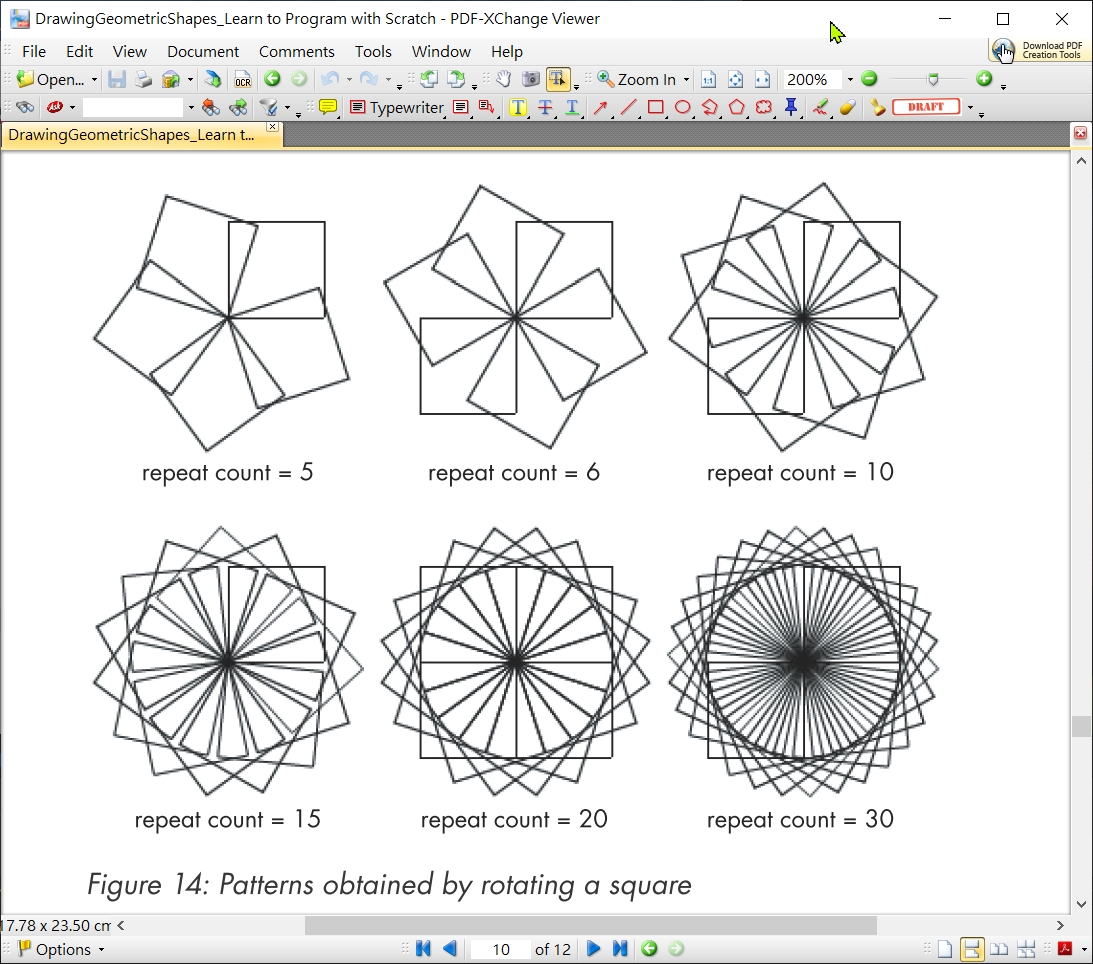旋轉正4邊形, 30重, 邊長100 >>>center_A_multiSameRegularPolygon(4, 30, 100)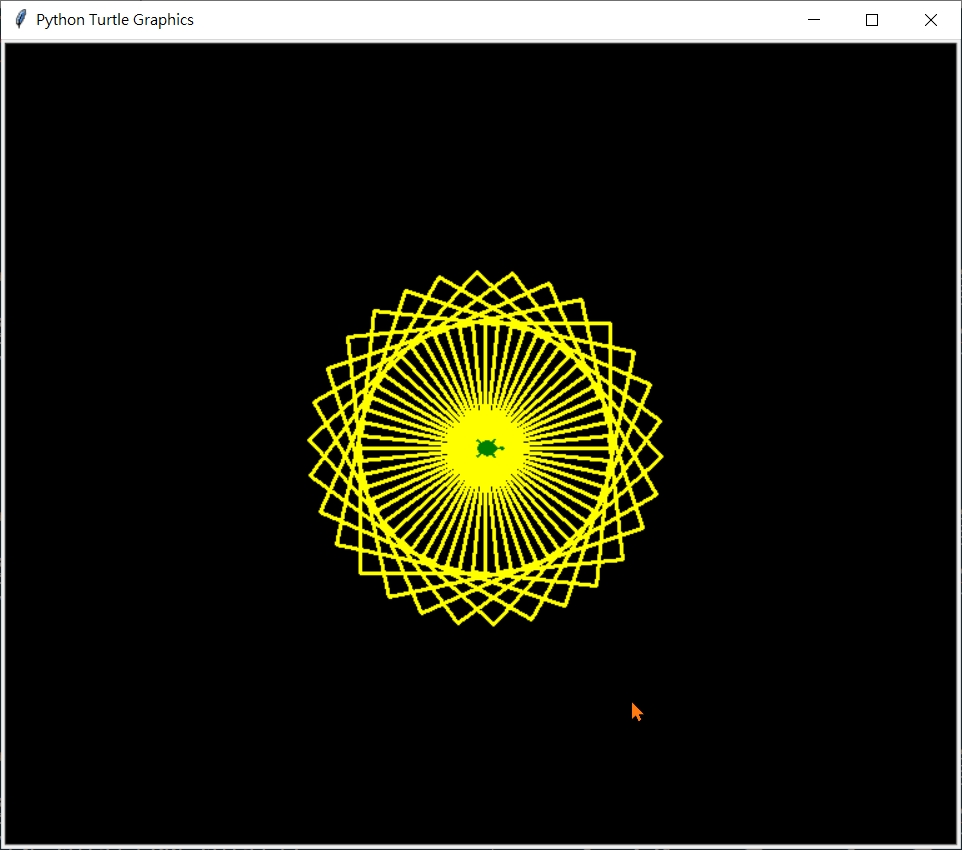

5.7.3 旋轉正5邊形

以下為旋轉正5邊形 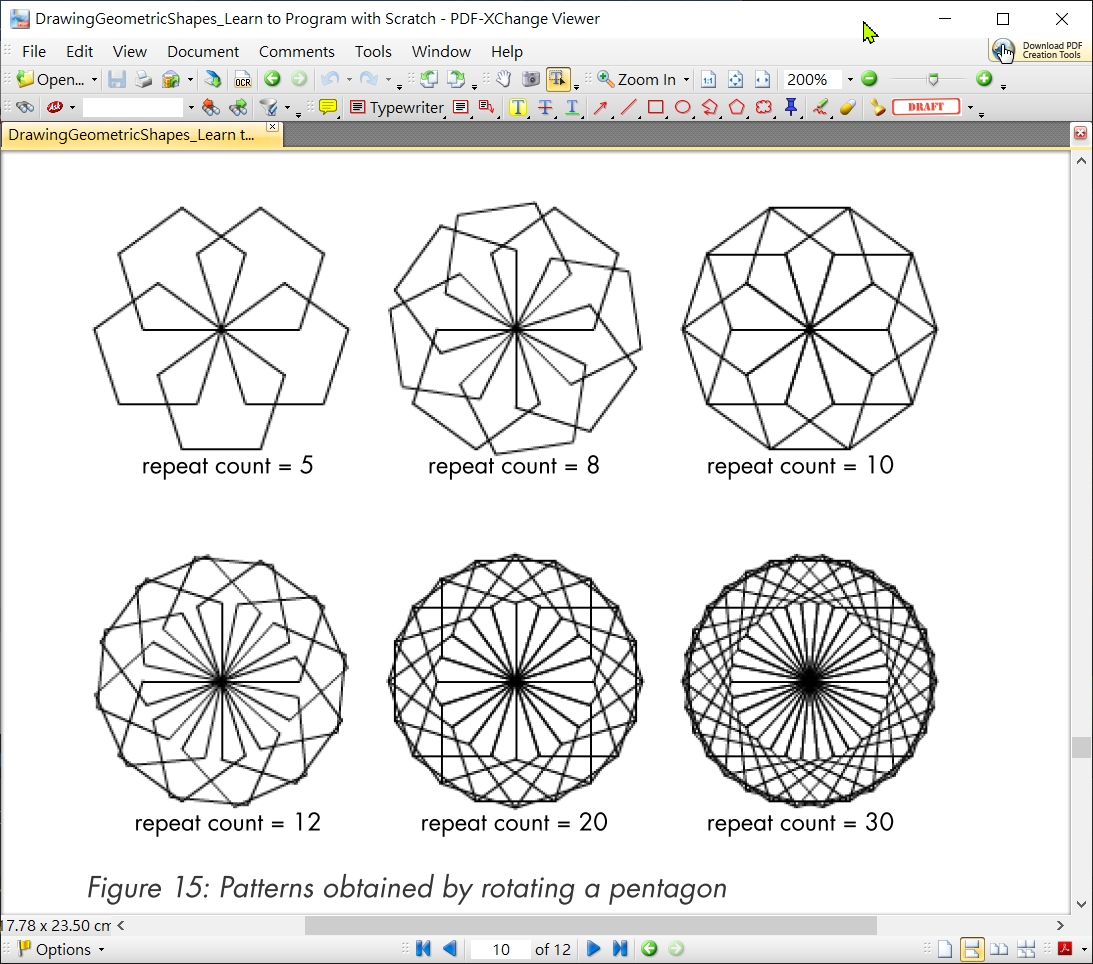旋轉正5邊形, 12重, 邊長100 >>>center_A_multiSameRegularPolygon(5, 12, 100)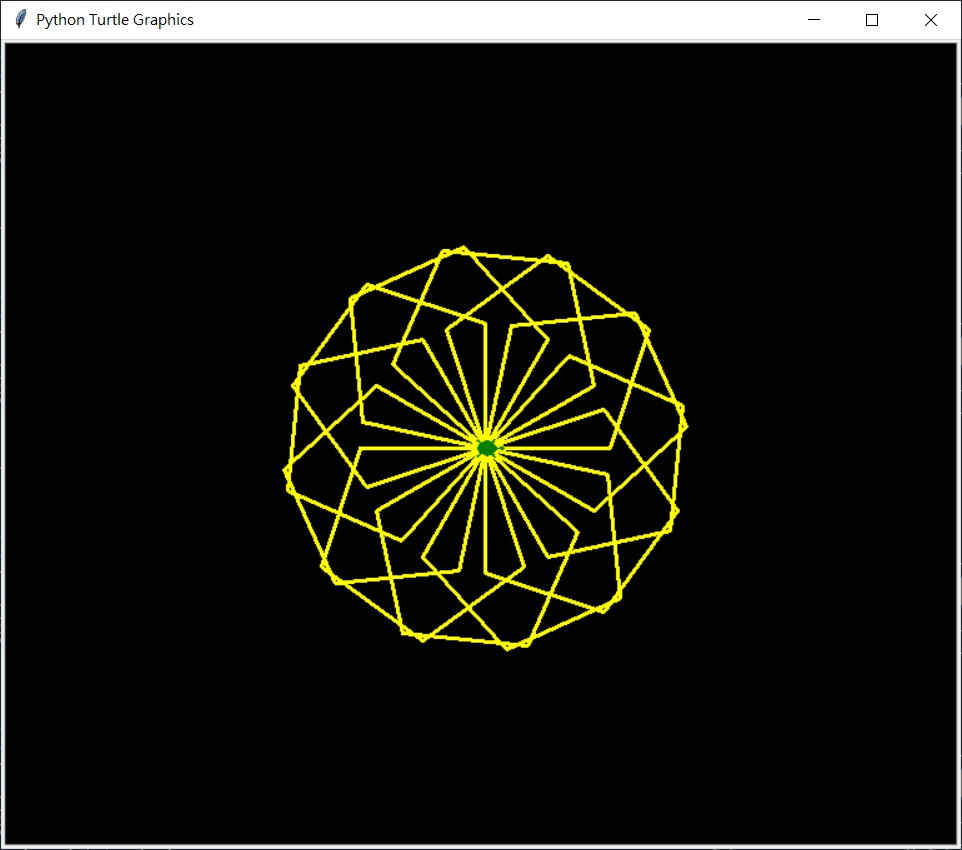

5.7.4 旋轉正6邊形

以下為旋轉正6邊形 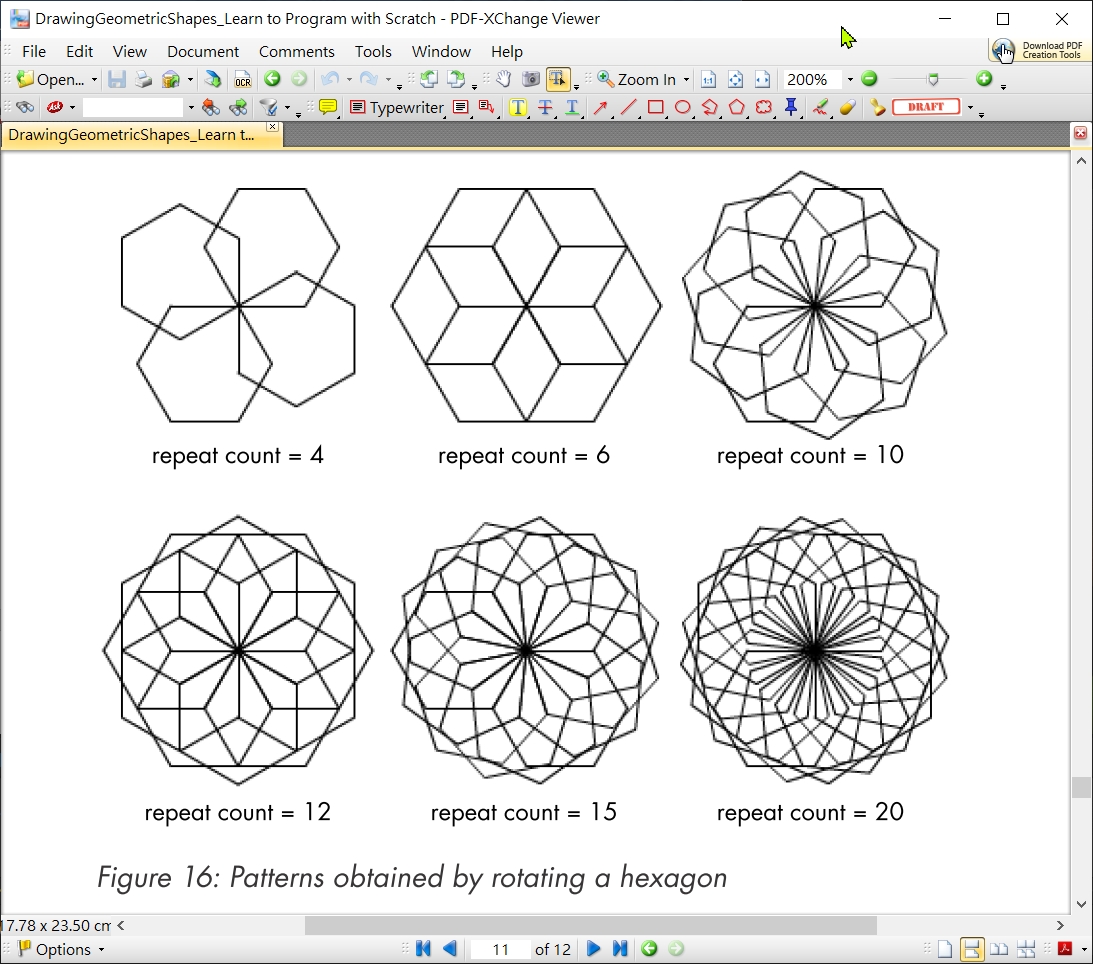旋轉正6邊形, 12重, 邊長100 >>>center_A_multiSameRegularPolygon(6, 12, 100)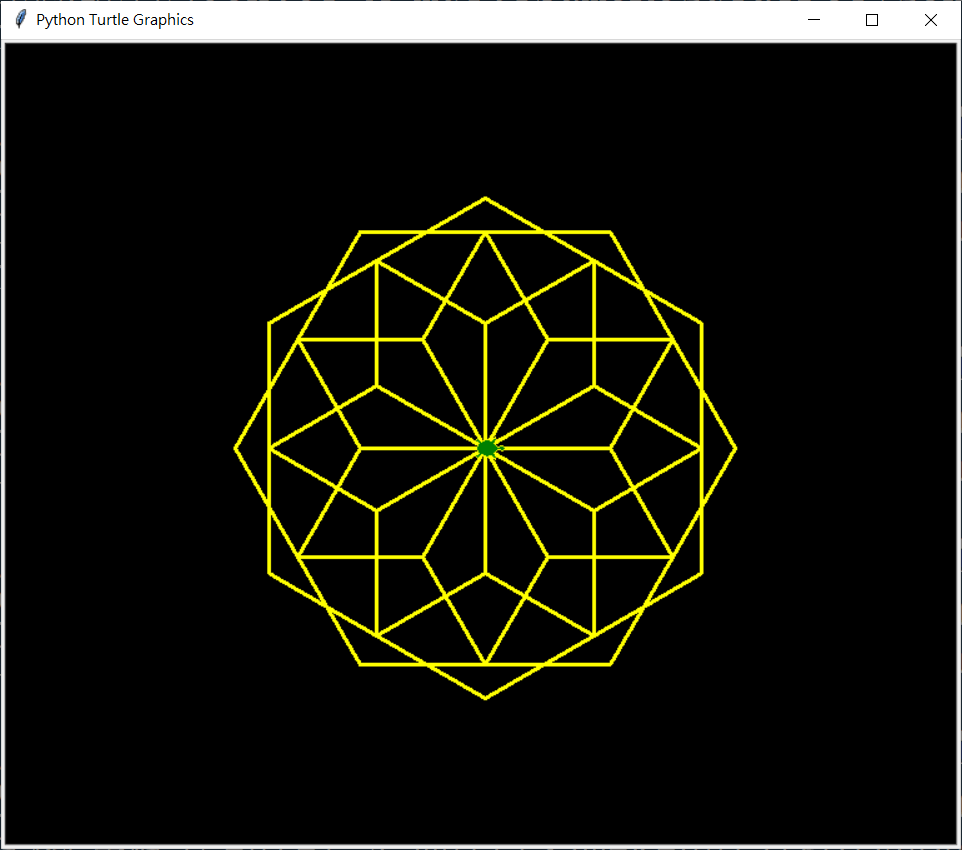

5.7.5 旋轉正7邊形

以下為旋轉正7邊形 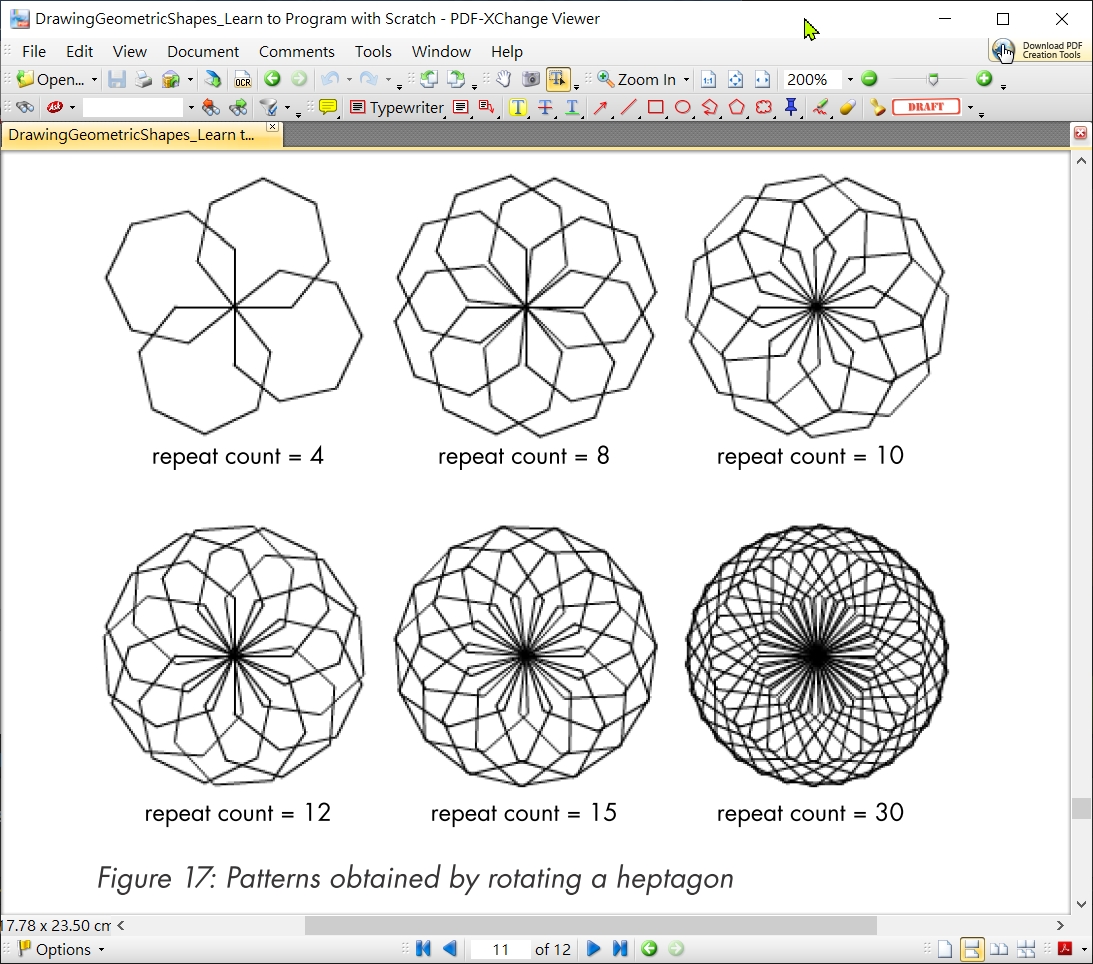旋轉正7邊形, 15重, 邊長100 >>>center_A_multiSameRegularPolygon(7, 15, 100)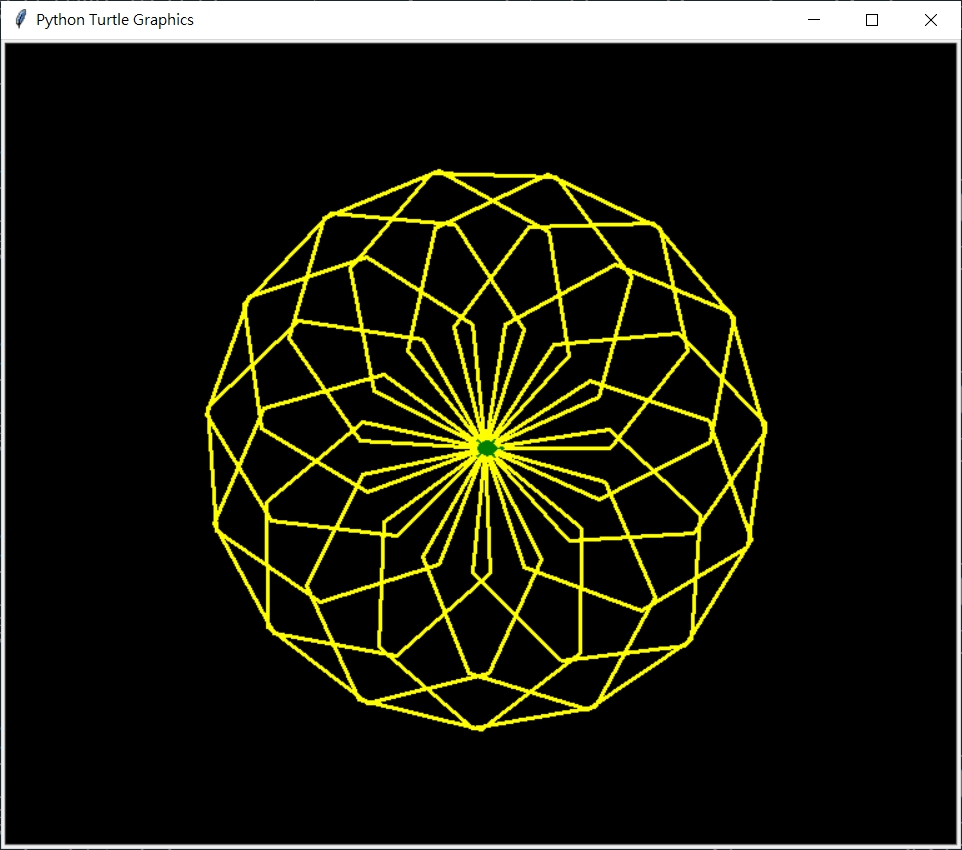

5.7.6 旋轉正8邊形

以下為旋轉正8邊形 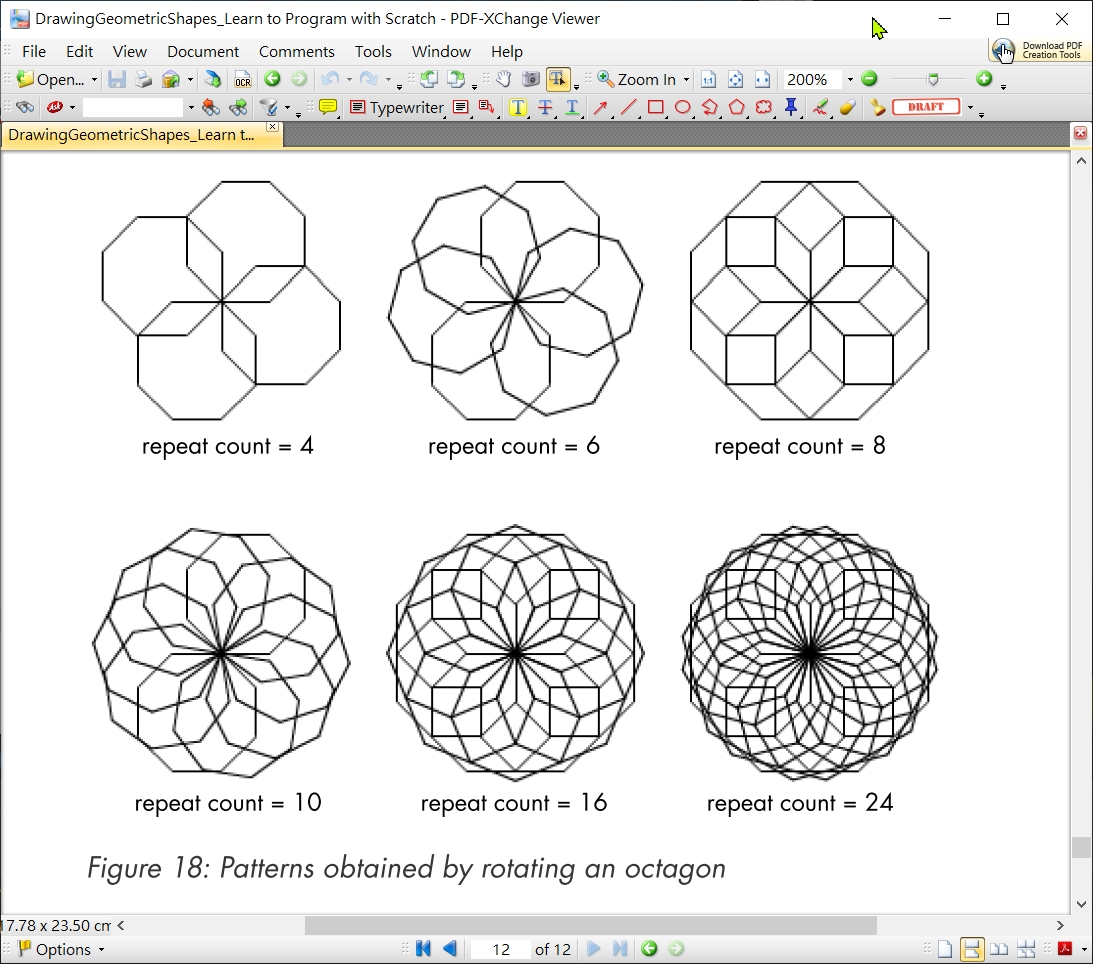旋轉正8邊形, 12重, 邊長100 >>>center_A_multiSameRegularPolygon(8, 12, 100)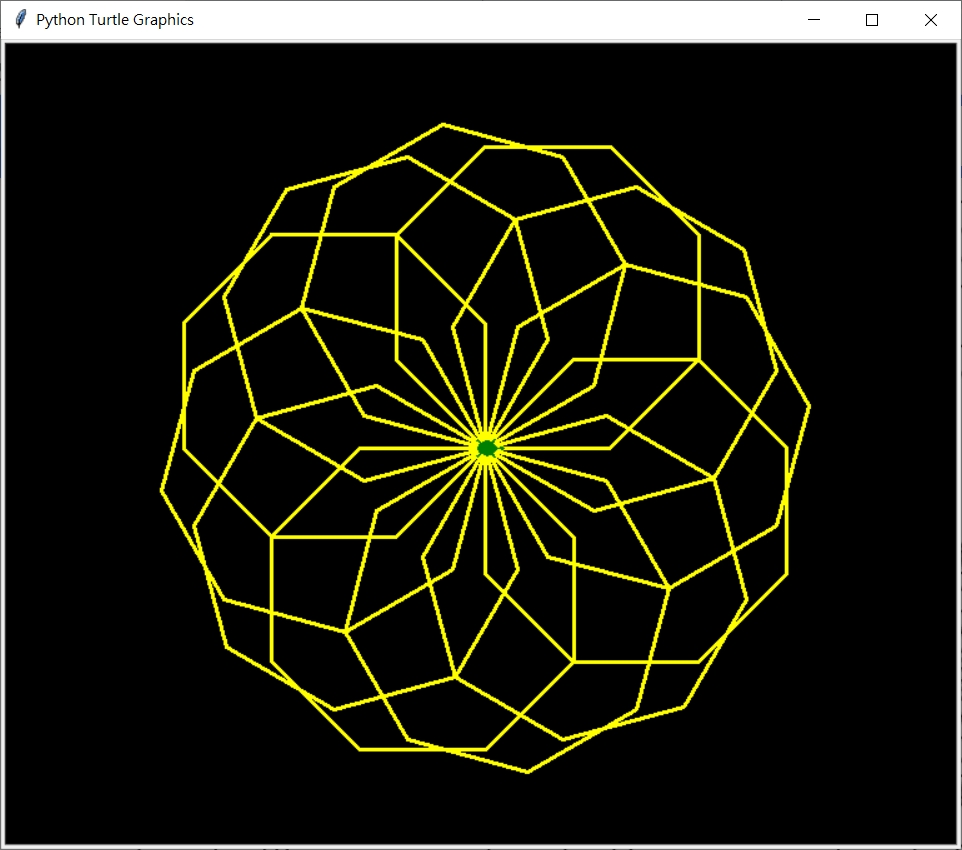

5.7.7 旋轉正9邊形

以下為旋轉正9邊形 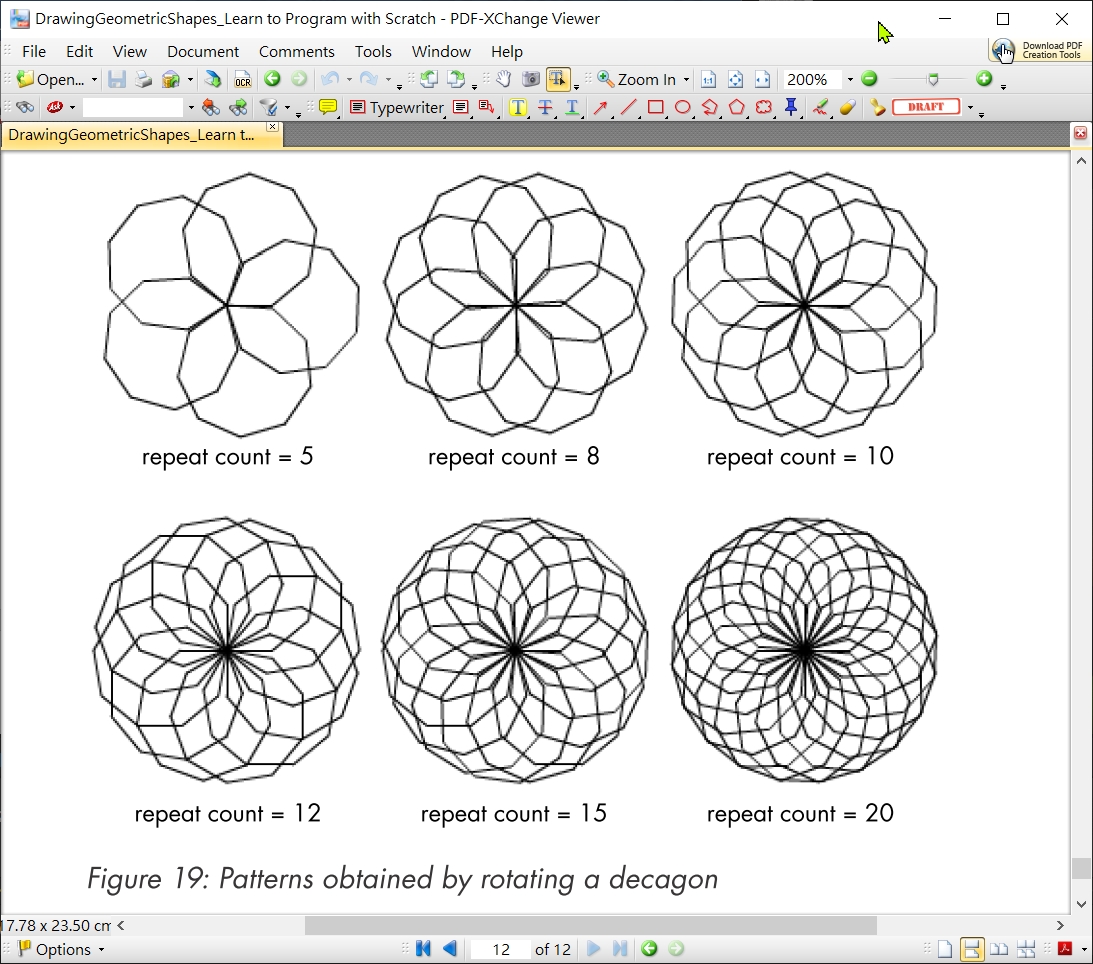旋轉正9邊形, 9重, 邊長100 >>>center_A_multiSameRegularPolygon(9, 9, 100)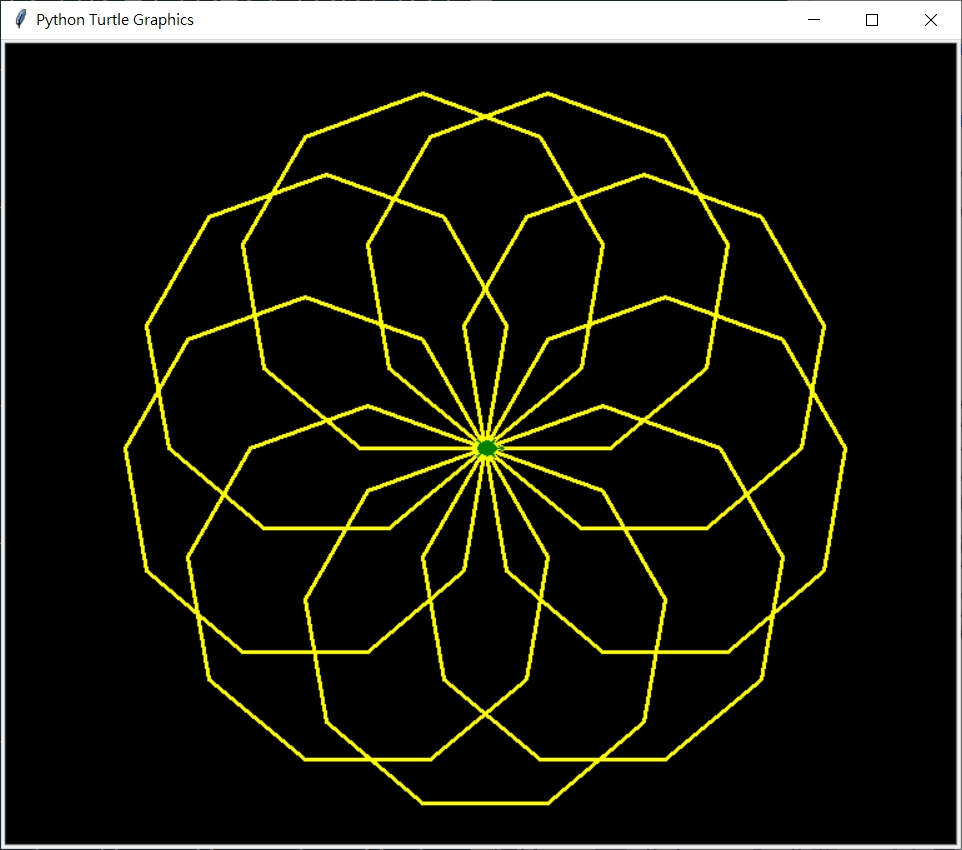

旋轉正9邊形, 27重, 邊長100 >>>center_A_multiSameRegularPolygon(9, 27, 100)